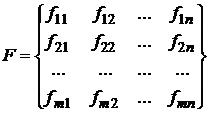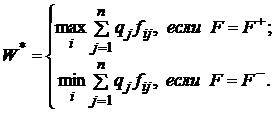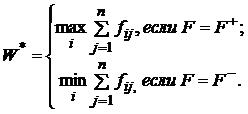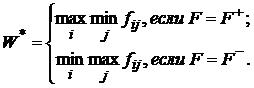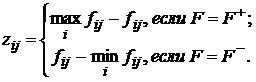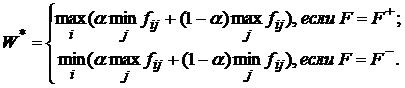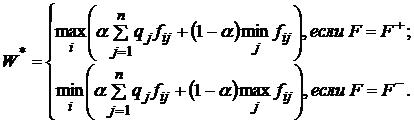| Главная » Статьи » Методические материалы » Примеры решения задач |
Для принятия оптимальных решений в условиях неопределенности используют математические модели, которые позволяют определенным способом формализовать процесс принятия решений, они дают возможность смоделировать конфликтную ситуацию или ситуацию с неопределенностью. Теория игр – это раздел современной математики, который изучает математические модели принятия решений в условиях неопределенности и конфликтности, т.е. в ситуациях, когда интересы контрагнетов либо противоположные, либо не совпадают. Игра – это формализованное описание (модель) конфликтной ситуации, которая включает в себя четко определенные правила действий ее участников, которые стараются победить, избирая конкретную стратегию поведения. При этом ни один из игроков не знает, какую стратегию изберет другой, но может количественно оценить эффективность результата реализации избранной стратегии. Стратегией игрока называется совокупность правил, которые определяют выбор варианта действий в каждой конкретной ситуации. Оптимальной стратегией игрока называется та стратегия, которая обеспечивает ему максимальный возможный выигрыш. Теория игр предусматривает наличие двух «игроков» - противников, при чем, поведение их друг для друга неизвестно. В экономике часто приходится принимать решения, в условиях недостаточной осведомленности относительно ситуации, в которой приходится действовать. В таких случаях результаты игры (выигрыш или проигрыш) зависит от неизвестной заранее объективной реальности, которую в теории игры принято называть природой, а соответствующую ситуацию - играми с природой. Природа рассматривается как незаинтересованная инстанция, стратегия поведения которой неизвестно, но она сознательно не противодействует нашим планам. Составляющими игры есть: 1. Первый игрок (или лицо, которое принимает решение (ЛПР)), который может принять решение из множества:
или множества чистых стратегий. Одна из этих стратегий обязательно должна быть избранна. 2. Второй игрок - в экономике, например, - это макро- и микросреда, которая находится в одном из попарно несовместимых состояний из множества:
одно из которых обязательно настанет. 3. Функционал оценивания - платежная матрица количественных оценок эффективности результата реализации множества стратегий ЛПР (первого игрока) при условии реализации стратегий второго игрока, например, определенного состояния экономической среды.
где: fij - количественная оценка деятельности первого игрока в случае, когда он избрал стратегию si, а второй игрок – стратегию Θj. Этапы игры:
Методы нахождения оптимальных стратегий Поскольку любая игровая задача представленная в матричной форме то можно говорить о поиске оптимальной стратегии. Решением игры – есть нахождение седловой точки. Т.е. нахождение стратегии, при которой наибольший из минимальных выигрышей игрока S точно равняется наименьшему из максимальных выигрышей игрока Θ, т.е. минимум в какой-нибудь строке матрицы совпадает с максимумом в каком-нибудь столбце. Для определения седловой точки нужно установить нижнюю и верхнюю цену игры. Например, имеем платежную матрицу (табл. 1)
Нижней ценой игры называется элемент матрицы, для которого выполняется условие:
где: i, j соответственно строки и столбцы матрицы. Нижняя цена игры показывает, что какую бы стратегию не применял игрок Θ, игрок S гарантирует себе выигрыш, не меньше чем α. В матрице 4 нижней ценой игры будет:
Верхней ценой игры называется элемент, который удовлетворяет условие:
Верхняя цена игры гарантирует для игрока Θ, что игрок S не получит выигрыш, больший чем β. Точка (элемент) матрицы, для которой выполняется условие:
и называется седловой точкой. Когда матрица имеет седловую точку и при условии максимальной разумности игроков, то именно эта точка и будет оптимальной стратегией. Но, наиболее распространенной является ситуация, когда матрица не имеет седловой точки. Формальная составляющая принятия решения в условиях неопределенности включает в себя знание критериев, на основе которых и осуществляется принятие решения, а также правила выбора одного из них, в соответствии с имеющейся у ЛПР информации. Критерии Байеса и Лапласа. Используется в том случае, когда заранее известно распределение вероятностей состояний внешней среды, или поведения неприятеля.
где: qj - вероятность состояния внешней среды. Критерием принятия решения в данном случае есть критерий Байеса: оптимальной считается такая стратегия si0, для которой W(i0) = W*, где W* - цена игры при выборе оптимальной стратегии (в понимании того или другого критерия), а W(i) - цене игры при выборе стратегии si.
В форме F = F+ функционал оценивания рассматривается для оптимизации выигрыша, а в форме F = F- в случае оптимизации потерь, ущерба и т.п. Если вероятность всех состояний внешней среды одинаковые , т.е. qj = 1/n(θj), то используется критерий Лапласа: оптимальной считают такую стратегию si0, для которой W(i0) = W*, где:
Критерии Вальда и Севиджа. Этот критерий применяется в том случае, когда решение принимается в условиях конкуренции, т.е. предполагается, что противник злонамеренный и действует целенаправленно. Чаще всего в такой ситуации применяют критерий Вальда, где оптимальной считают такую стратегию si0, для которой W(i0) = W*, где:
Данный критерий безрисковый, поскольку учитывает наиболее плохую ситуацию. Критерий Вальда иногда используют несколько в другой форме. Сначала из платежной матрицы F образовывают другую матрицу Z той же размерности по следующему правилу:
Дальше для определения оптимальной стратегии к матрице Z применяют критерий Вальда. Поскольку независимо от ингредиента платежной матрицы F, Z = Z-, то формулирование полученного критерия, который носит название критерий Севиджа будет следующим: оптимальной считают такую стратегию si0, для которой W(i0) = W*, где:
Критерий Гурвица и Хеджеса-Лемана применяется в ситуации, относительно которой неизвестны распределения вероятностей состояния внешней среды, но можно сделать некоторые прогнозы относительно реализации лучшего или худшего сценария. Пусть α є [0;1] - некоторый заведомо заданный параметр (прогноз состояния внешней среды). Тогда по критерию Гурвица оптимальной считают такую стратегию si0, для которой W(i0) = W*, где:
В данном критерии учтено как самый пессимистический, так и самый оптимистичный прогнозы. В частности при α = 1 получаем критерий Вальда (пессимистический прогноз), а при α = 0 - критерий наилучшего результата (оптимистичный прогноз). Соответственно по критерию Ходжеса-Лемана оптимальной считают такую стратегию si0, для которой W(i0) = W*, где:
Пример решения задач: У фирмы, которая продает кондитерскую продукцию, на протяжении 20 дней два раза было куплено 10 упаковок товара, шесть раз - 12 упаковок, семь раз - 15 упаковок, пять раз - 16 упаковок. Необходимо определить, какой должна быть оптимальная величина дневного запаса товара, если закупочная цена одной упаковки составляет 4,5 грн, а цена реализации 6 грн. Непроданная на протяжении одного дня кондитерская продукция подлежит обязательной утилизации. Решение Пользуясь исходными данными, строим матрицу выигрышей (табл. 2), строки этой матрицы будут содержать возможные варианты стратегий, а столбцы - возможные варианты окружающей среды (количество упаковок, которую нужно закупать фирме и количество проданных упаковок). Выигрышами в каждом случае будет возможная прибыль.
Прибыль Pij от продажи продукции рассчитываем по формуле:
где Dj – доход от продажи j-го количества упаковок; Ci – стоимость i-го количества упаковок. Если j > i, то принимается, что j = i.Оптимальное количество упаковок, которое нужно закупать, находим на основе максимизации ожидаемой прибыли M(Pi) → max, что соответствует критерию Байеса. Для этого рассчитываем значение математического ожидания прибыли для разного количества закупаемых упаковок продукции. В первом случае M(P1) = 15. Во втором случае M(P2) = 11,4. В третьем случае M(P3) = 14,1. В четвертом случае M(P4) = 11,1. Соответственно заданному условию оптимизации находим значение математического ожидания прибыли:
Ответ: оптимальной стратегией для фирмы будет формировать дневной запас от 10 до 12 упаковок продукции. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 15200 | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||