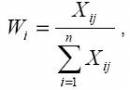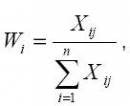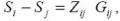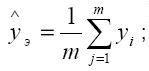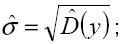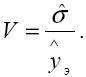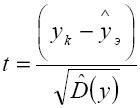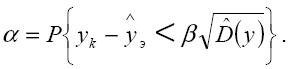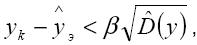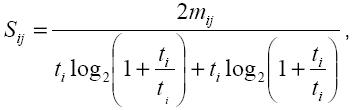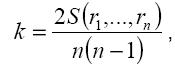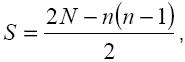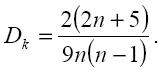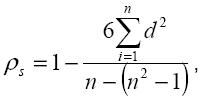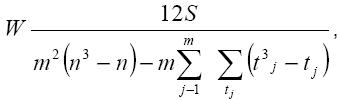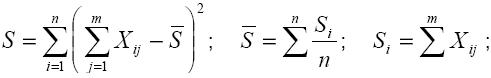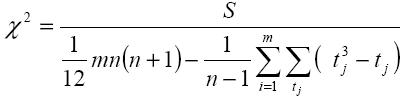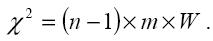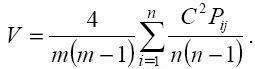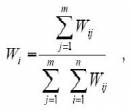
1. Введение

Рост масштабов и темпов развития экономики, необходимость повышения ее эффективности и качества работы предъявляют новые более высокие требования к методам управления. В процессе управления мы непрерывно сталкиваемся с необходимостью принимать решения на различных иерархических уровнях. Обычно задача выбора решается в условиях неопределенности либо неопределенность составляет существо задачи (например, при анализе многоуровневых и многофакторных систем).

Существенным фактором повышения качества принимаемых решений является применение математических методов и моделей. Однако полная математическая формализация технико-экономических задач часто неосуществима вследствие их новизны и сложности. В таких ситуациях, когда необходимо сделать правильный выбор, а обоснование и оценка последствий решений не могут быть выполнены на основе точных расчётов, применяются экспертные методы, под которыми понимают комплекс логических и математико-статистических методов и процедур, направленных на получение от специалистов информации, необходимой для подготовки и выбора рациональных решений [1].

В настоящее время разработано достаточно большое количество математико-статистических методов экспертных оценок и вычислительных алгоритмов [1–7]. ...

2. Методы обработки информации

Данные методы решают задачу преобразования информации, получаемой от экспертов, в форму, удобную для дальнейшего анализа, направленного на подготовку и принятие рационального решения. Обработка информации, получаемой от экспертов, наиболее часто производится методами непосредственной оценки, ранжирования и парных сравнений, краткое описание которых приведено ниже. ...

Метод непосредственной оценки

Метод непосредственной оценки используется в случаях, когда обеспечивается чёткое различие между альтернативами и (или) альтернативы поддаются непосредственному измерению, так как имеют одинаковую природу.

Диапазон изменения какой-либо качественной переменной разбивается на несколько интервалов, каждому из которых присваивается определённая оценка (балл), например, от 0 до 10. Задача эксперта заключается в помещении каждой из рассматриваемых альтернатив в определённый оценочный интервал в соответствии со степенью обладания тем или иным свойством либо в соответствии с предположениями эксперта об их значимости. Заметим, что число интервалов, на которые разбивается весь диапазон изменения качества, не обязательно должно быть одинаково для каждого эксперта. Кроме того, каждому эксперту разрешается давать одну и ту же оценку двум (или нескольким) качественно различным альтернативам. Составляется матрица "эксперты – альтернативы", в которой проставляются полученные от каждого эксперта оценки альтернатив по шкале от 0 до 10. Рассчитывается относительная значимость всех альтернатив в отдельности для каждого эксперта. С этой целью оценки, полученные от каждого эксперта, по всем альтернативам суммируются, а затем нормируются. Нормирование любой меры означает, что представляющее её число для всего множества в целом принимается равным единице. Нормирование позволяет установить более тесную связь между оценками, приписанными экспертами отдельным альтернативам. Вычисляется усреднённая оценка, данная всеми экспертами по каждой альтернативе. Для этого нормированные оценки каждой альтернативы, полученные в предыдущем шаге, суммируются, а затем полученная сумма делится на число экспертов. Таким образом рассчитывается средняя арифметическая оценка для каждой альтернативы по формуле:

(1)

где: W_ij– вес i -й альтернативы, подсчитанный по оценкам всех экспертов.

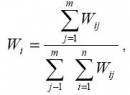
где: X_ij – оценка альтернативы i , данная экспертом j , n – число альтернатив, m – число экспертов.

Метод ранжирования

Может применяться в следующих ситуациях:

• когда необходимо упорядочить альтернативы во времени или пространстве. Это ситуация, когда интересуются не сравнением степени выраженности какого-либо их качества, а лишь взаимным пространственным или временным расположением этих альтернатив;

• когда нужно упорядочить альтернативы в соответствии с каким-либо качеством, но при этом не требуется производить его точное измерение;

• когда какое-либо качество в принципе измеримо, однако в настоящий момент не может быть измерено по причинам практического или теоретического характера.

Метод ранжирования редко используется "в чистом виде". Чаще всего он сочетается с другими методами, обеспечивающими более чёткое различие между альтернативами. Одним из них является метод непосредственной оценки. В некоторых случаях оказывается удобнее для выбора наиболее предпочтительной альтернативы сначала произвести оценку, а затем – ранжирование.

Суть процедуры ранжирования заключается в том, что эксперт располагает альтернативы в порядке, который представляется ему наиболее рациональным, и приписывает каждой из них числа натурального ряда – ранги. При этом ранг 1 получает наиболее предпочтительная альтернатива, а ранг N – наименее предпочтительная.

Следовательно, порядковая шкала, получаемая в результате ранжирования, должна удовлетворять условию равенства числа рангов N числу ранжируемых альтернатив n.

Эксперт может присваивать один и тот же ранг нескольким альтернативам, и в результате число рангов N оказывается не равным числу ранжируемых альтернатив n. В таких случаях альтернативам приписывают "стандартизованные" ранги. С этой целью общее число стандартизованных рангов полагают равным n, а альтернативам, имеющим одинаковые ранги, присваивают стандартизованный ранг, значение которого представляет среднее суммы мест, поделенных между собой альтернативами с одинаковыми рангами.

Вычисляется усреднённая оценка, данная всеми экспертами по каждой альтернативе:

(2)

где:W_ij– вес i-й альтернативы, подсчитанный по оценкам всех экспертов.

где:X_ij- оценка альтернативы i , данная экспертом j, n – число альтернатив, m – число экспертов.

Наиболее предпочтительным будет альтернатива, имеющая наименьшую усреднённую оценку (вес).

Метод парных сравнений

Парное сравнение производится, когда число альтернатив велико, и в тех случаях, когда различия между альтернативами настолько малы, что непосредственная оценка или ранжирование не обеспечивают их разумного упорядочения.

Таким образом, метод парных сравнений имеет некоторое преимущество перед другими методами упорядочения в случаях, когда альтернатив много и (или) они трудно различимы.

В методе парных сравнений альтернативы сопоставляются попарно экспертом (экспертами), а затем выбирается одна из них наиболее важная. В этом случае эксперт предпочитает данную альтернативу, хотя выбор не обязательно будет выражать его предпочтение. В общем случае эксперт может установить равенство альтернатив или зафиксировать свои предпочтения на некоторой шкале. За основу берут результаты ранговой оценки альтернатив. Основной элементарный акт – сравнение двух альтернатив A и B одним экспертом – можно распространить на случай, когда несколько экспертов рассматривают более чем две альтернативы. Результаты этой процедуры можно представить в виде матрицы A предпочтений с элементами X_ij, равными числу случаев, когда A_i предпочтительней, чем A_j. На основе матрицы A строится матрица P, показывающая соотношение случаев, когда альтернатива i более предпочтительна, чем альтернатива j. Элементы матрицы Р обладают тем свойством, что P_ij=X_ij/m где m – число экспертов, а также P_ij+P_ji=1 В матрице P элементы P_ij представляют относительное число предпочтений, полученных от всех экспертов по каждой альтернативе перед каждой другой альтернативой. Разности между шкальными оценками двух альтернатив можно выразить с помощью модели шкалы:

где: S_i, S_j – шкальные оценки альтернатив;

Z_ij – нормированное отклонение, соответствующее j (для случаев предпочтения альтернативы i альтернативе j );

G_ij – стандартное (среднее квадратичное) отклонение предполагаемого распределения различий между S_i и S_j.

При этом предполагается, что G_ij = 1 и тогда S_i - S_j = Z_ij. атем по таблицам нормированного нормального распределения ищут значение Z_ij для величины P'_ij = P_ij - 0,500 и составляется матрица Z основного преобразования. Конструируется следующая матрица, значения оценок которой находятся путём вычитания каждой записи j ряда матрицы Z_ij из полученной оценки S_i. Средняя величина ряда в этой матрице – это шкальная оценка соответствующей альтернативы.

Метод комплексной экспертной оценки

Применяется во всех случаях, когда из исследуемой совокупности альтернатив необходимо выбрать наиболее существенный, а выбор конкретного метода решения затруднителен [7].

Для получения комплексной экспертной оценки составляется матрица “эксперты – альтернативы", где в роли экспертов выступают методы решений (непосредственная оценка, ранжирование и парные сравнения), а в качестве их оценок – результаты решений этими методами. Затем, в качестве метода «вторичной» обработки полученной информации, применяется метод ранжирования, если количество оцениваемых альтернатив k < 10, либо метод парных сравнений, если k > 10.

3. Анализ экспертной информации

Анализ согласованности ответов экспертов предназначен для проверки достоверности экспертных оценок и выявления причин их неоднородности с помощью статистической обработки информации, полученной от экспертов [8].

Статистические характеристики

Полученные от экспертов оценки могут рассматриваться как случайная переменная. Поэтому для анализа разброса и согласованности оценок применяются обобщённые статистические характеристики:

а) среднее значение оценок (точечная оценка для данной группы экспертов), которое характеризует обобщённое мнение экспертов по альтернативам. Для альтернативы S:

(3)

б) среднее квадратичное отклонение, характеризующее разброс мнения отдельных экспертов относительно среднего значения ÿ_э. Для альтернативы S

(4)

в) коэффициент вариации, характеризующий вариабельность, рассчитываемую в виде отношения среднего квадратичного отклонения к средней арифметической. Для альтернативы S

(5)

Аналогично вычисляются результаты по другим альтернативам.

Противоречивость мнений

С точки зрения математической статистики, исходные оценки y_i , далеко отстоящие от среднего значения ÿ_э, могут считаться случайными. Введём понятие противоречивости мнения эксперта k обобщённому мнению всех экспертов. Допустим, что мнение y_k эксперта k является крайним среди мнений m экспертов. Анализ противоречивости мнения эксперта k проводится с использованием оценки анормальности результатов при неизвестной генеральной дисперсии, суть которого заключается в следующем. Сначала вычисляется вероятность того, что величина:

(6)

превзойдёт некоторый заданный максимум β:

(7)

Если эта вероятность достаточно велика (например, больше 0,05 – 0,10), то гипотеза об анормальности y_k может быть отброшена, в противном случае – принята. В связи с этим "противоречивым" будем считать мнение эксперта y_k, при котором выполняется неравенство:

(8)

с вероятностью, меньшей некоторого предела α'. Обычно за α' принимают величину порядка 0,05 и менее. Если неравенство не выполняется, значит, мнение эксперта не противоречиво.

Коэффициенты ассоциации (по Устюжанинову)

Используются для оценки меры сходства мнений каждой пары экспертов. С помощью коэффициентов ассоциации учитывается лишь число совпадающих или несовпадающих ответов и не учитывается их последовательность [1].

Информационная мера близости ответов двух экспертов, предложенная В.Л. Устюжаниновым, вычисляется по следующей формуле:

(9)

где m_ij – количество признаков, одинаково оценённых i - m и j - m экспертами;

t_i – количество признаков, оценённых i - m экспертом;

t_j – количество признаков, оцененных j - m экспертом.

Величина S_ij меняется в пределах от 1 до 0, причём S_ij = 1 указывает на полное совпадение мнений опрашиваемых, а S_ij = 0 – на полное различие мнений.

Коэффициент ранговой корреляции Кендалла

Одна из выборочных мер зависимости двух случайных величин (признаков) X и Y основана на ранжировании элементов выборки (X₁,Y₁),...,(X_n,Y_n). Коэффициент ранговой корреляции Кендалла [9] относится, таким образом, к ранговым статистикам и определяется формулой

(10)

где r_i – ранг Y, принадлежащий той паре (X ,Y), для которой ранг X равен i,

N – число элементов выборки, для которых одновременно j < i и r_j < r_i. Всегда -1 ≤ k ≤ 1.

Коэффициент ранговой корреляции Кендалла применяется для проверки гипотезы независимости случайных величин.

Если гипотеза независимости верна, то Ek = 0 и

При небольшом объёме выборки (4 ≤ n ≤ 10) проверка статистической гипотезы независимости производится с помощью специальных таблиц. При n > 10 пользуются нормальным приближением для распределения k.

Коэффициент ранговой корреляции Кендалла, как и любая ранговая статистика, может использоваться для обнаружения зависимости двух качественных признаков, если только элементы выборки можно упорядочить относительно этих признаков.

Коэффициент ранговой корреляции Спирмена

Мера зависимости двух случайных величин (признаков) X и Y, основанная на ранжировании независимых результатов наблюдений (X₁,Y₁),...,(X_n,Y_n). Если ранги значений X расположены в естественном порядке i = 1,..., n, а R_i – ранг Y , соответствующий той паре (X ,Y ), для которой ранг X равен i, то коэффициент ранговой корреляции Спирмена [1] определяется формулой:

(11)

где d_i – разность между рангами X_i и Y_j. Значение ρ_s меняется от -1 до +1, причём ρ_s = +1, когда последовательности рангов полностью совпадают, т.е. i = R_i, i = 1,...,n. Коэффициент ранговой корреляции Спирмена, как и любая другая ранговая статистика, применяется для проверки гипотезы независимости двух признаков. Если признаки независимы, то E_{ρ s} = 0, D_{ρ s} =1 / n - 1. Таким образом, по величине отклонения ρ s от нуля можно сделать вывод о зависимости или независимости признаков.

Конкордация

При анализе оценок, полученных от экспертов, часто возникает необходимость выявить согласованность их мнений по нескольким альтернативам, оказывающим влияние на один конечный результат. В этом случае согласованность мнений экспертов оценивается с помощью коэффициента конкордации, т.е. общего коэффициента ранговой корреляции для группы, состоящей из m экспертов [1].

Ранжированные оценки

Коэффициент конкордации определяют по формуле:

(12)

где S – сумма квадратов разностей /отклонений/;

n – число альтернатив;

m – число экспертов;

X_ij – ранг i-й альтернативы, присвоенный ему j-м экспертом;

t_j – число одинаковых рангов, которые присваивает разным альтернативам j-й эксперт.

Таким образом, для того чтобы оценить значимость коэффициента конкордации, пользуются критерием χ-квадрат:

(13)

или

(14)

Найденное значение должно быть больше табличного χ-квадрат, определяемого числом степени её свободы и уровнем доверительной вероятности. Это подтверждает значимость коэффициента конкордации.

Парные сравнения

Для определения коэффициента конкордации составляется матрица предпочтений, в которой числа P_ij показывают, сколько раз альтернатива i была предпочтительнее альтернативы j по мнению m экспертов. В результате проведения Cn² таких сравнений отдаётся предпочтение каким-то 1/2 Cn² альтернативам по сравнению с остальными 1/2 Cn² альтернативами. Очевидно, что при полном согласии m экспертов Cn² ячеек матрицы будут содержать число q = m , а в остальных ячейках будут нули. При минимальном согласии каждая ячейка будет содержать q = 1/2 m, если число экспертов чётное, и q = 1/2 (m + - 1), если оно нечётное. Исходя из этого, коэффициент согласия при парном сравнении определяется по формуле:

(15)

Таким образом, для того чтобы оценить значимость коэффициента конкордации, пользуются критерием χ-квадрат:

(16)

Найденное значение должно быть больше табличного χ-квадрат, определяемого числом степеней свободы и уровнем доверительной вероятности. Это подтверждает значимость коэффициента конкордации. ...

... Исследование состоит из нескольких этапов: ввод исходных данных, анализ их согласованности и достоверности, обработка мнений экспертов (решение), визуализация.

Анализ проводится непосредственно пользователем с целью определения качества исходных данных. В первую очередь необходимо оценить согласованность мнений экспертов. Согласованность показывает, являются ли мнения экспертов "белым шумом" или отражают некоторую существующую устойчивую закономерность.

Для оценки согласованности применяется коэффициент конкордации:

– коэффициент согласия при парном сравнении;

– дисперсионный коэффициент – для ранжированных рядов.

Если расчетное значение критерия "χ-квадрат" для данного коэффициента конкордации больше табличного, то мнения экспертов согласованы.

В случае, если мнения оказались согласованы, то дальнейший анализ можно не проводить при условии, что у пользователя нет на то особых причин. При наличии несогласованности мнений экспертов целесообразно продолжить анализ для выявления причин их неоднородности.

Проводится проверка на непротиворечивость мнений, в ходе которой выявляются эксперты, мнения которых существенно отличаются от общего мнения группы.

Для оценки меры сходства мнений каждой пары экспертов могут быть использованы различные методы.

Наиболее грубый подход основан на расчете коэффициентов ассоциации, с помощью которых учитывается лишь число совпадающих и несовпадающих ответов и не учитывается их последовательность.

Более точную проверку согласованности пар мнений экспертов можно провести, используя методы ранговой корреляции Кендалла и Спирмена. Отметим, что метод расчета коэффициента ранговой корреляции, предложенный Спирменом, вычисляется проще и быстрее.

Кроме того, при необходимости пользователь может оценить часто используемые статистические характеристики:

– математическое ожидание;

– среднее квадратичное отклонение;

– коэффициент вариации. ...

Для выбранного метода результатом решения будет вектор оценок, присвоенный каждой альтернативе. Эта информация является основой для принятия решения о предпочтительности той или иной рассмотренной альтернативы.

СПИСОК ЛИТЕРАТУРЫ

1. Бешелев С.Д., Гурвич Ф.Г. Математико-статистические методы экспертных оценок. – М.: Статистика, 1980. – С. 263.

2. Бешелев С.Д., Карпова И.В. Выбор перспективной техники с помощью метода экспертных оценок // Экономика и математические методы. – 1972. – Т. VIII. – Вып. 1. – С. 82.

3. Теория выбора и принятия решений / И.М. Макаров, Т.М. Виноградская, А.А. Рубчинский и др. – М.: Наука, 1982. – C. 328.

4. Евланов Л.Г., Кутузов В.А. Экспертные оценки в управлении. – М.: Экономика, 1978. – С. 133.

5. Китаев Н.Н. Групповые экспертные оценки. – М.: Экономика, 1975. – С. 64.

6. Бешелев С.Д., Гурвич Ф.Г. Экспертные оценки в принятии плановых решений. – М.: Экономика, 1976. – С. 79.

7. Лисецкий Ю.М. Метод комплексной экспертной оценки для проектирования сложных технических систем // Математичні машини і системи. – 2006. – № 2. – С. 141–146.

8. Литвак Б.Г. Экспертная информация: Методы получения и анализа. – М.: Радио и связь, 1984. – С. 118.

9. Кендалл М. Ранговые корреляции. – М.: Статистика, 1975. – С. 174.